If the best contingency we have is to slot students who missed exams into an unreliable grade ranking then we need to look again at the fundamentals, writes Dennis Sherwood
Despite assurances from ministers that exams will go ahead in England this academic year, the exams regulator and exam boards are nevertheless developing contingency plans. Given the disruption already caused by regional infection rates, and the hard-to-gauge impacts of a new national lockdown – albeit with schools remaining fully open – this seems to me to be wise.
However, one of the plans revealed this week is problematic: to use the grades awarded to students who have been able to take the exams as ‘milestones’, and then to ‘slot in’ those students who can’t sit them based on previously-determined teacher rankings.
Imagine a cohort of 100 students. Students ranked 35 and 37 sit the paper. Student 36 does not. If students 35 and 37 are awarded grade B, then student 36 is awarded grade B. Fine. But suppose student 35 gets a B, and 37, a C. Is student 36 awarded a B or a C?
More problematic still, suppose the exam grades are the inverse of the teacher’s rankings – it’s student 35 who is awarded a C and student 37 a B. In the teacher’s judgement, student 36 ranks higher than student 37 (implying the award to student 36 of a B, if not an A), and simultaneously below student 35 (implying C, if not D). Now that’s a real muddle…
There is no single, exact, ‘right’ mark for any script
How did this happen? Perhaps student 37 pulled out all the stops. Perhaps the teacher’s judgement was wrong (or biased?) and student 37 really is the best of the trio. Perhaps students 35, 36 and 37 (and 34 and 38 too) are much the same, and forcing a rank order was unreasonable.
But there is another possible explanation too: Perhaps the rank order determined by the exam is wrong.
That’s crazy! The Prime Minister himself said that “exams are the fairest and most accurate way to measure a pupil’s attainment”.
But as everyone reading this knows, there is no single, exact, ‘right’ mark for any script: one examiner (or team) might give a script, say, 64 marks, another, 66. Neither is ‘right’ or ‘wrong’; both are equally valid.
Yet under the current Ofqual policy for determining grades from marks, the grade is awarded according to the single mark given by whichever examiner happens to mark the script. This poses no problem if both marks are within the same banding. But if there is a grade boundary at 65, there is a very big problem indeed – hence Dame Glenys Stacey’s acknowledgement at the Select Committee hearing on 2 September that exam grades are “reliable to one grade either way”. Or in plainer language, 1 exam grade in every 4 is wrong, this being about 1.5 million wrong grades every year.
The primary purpose of marking scripts is to determine a student rank order. Ofqual then determines the grade boundaries to secure whatever distribution is required, according to policies such as ensuring comparative outcomes or fighting grade inflation. This mark-determined rank order therefore underpins the determination of grades. But the truth is that this rank order is a lottery, as illustrated by this chart showing the results of my simulation of the 2019 A level in geography.
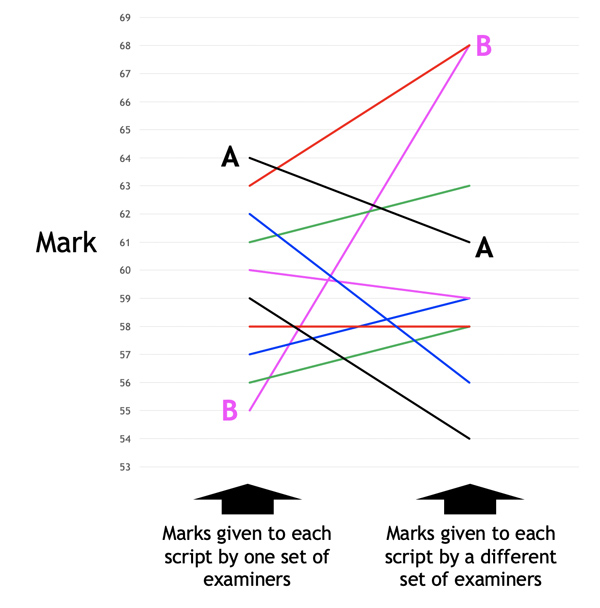
Ten scripts are each given a mark from 55 to 64, resulting in the rank order shown on the left: student A ranks highest; student B, lowest. If, however, those same scripts were marked by different examiners, the marks might be those on the right, resulting in a totally different rank order – this being just one example of very many.
In short, the rank order resulting from any examination as currently conducted is fundamentally unreliable. Awarding next summer’s grades by slotting the ‘missing grades’ within those determined by these exams is therefore fraught with danger.
Instead of the kind of piecemeal tinkering with the status quo that got us into trouble in summer 2020, there is an opportunity to fix the grade unreliability problem for good. That, to me, is the fairest and most reliable approach.








Your thoughts